2019下半年重庆教师资格证高中《数学学科知识与教学能力》真题及答案解析

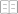
　　参考答案：A

　　参考解析：略

　　参考答案：A

　　参考解析：略

　　3.题目暂缺

　　参考答案：B

　　参考解析：略

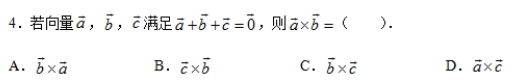
　　参考答案：C

　　参考解析：略

　　5.设n阶方阵M的秩r(M)=r

　　A.任意一个行向量均可由其他r个行向量线性表示

　　B.任意r个行向量均可组成极大线性无关组

　　C.任意r个行向量均线性无关

　　D.必有r个行向量线性无关

　　参考答案：D

　　参考解析：略

　　6. 试题暂缺，参考答案C

　　7.下列对向量学习意义的描述:

　　①有助于学生体会数学与现实生活和其他学科的联系;

　　②有助于理解数学运算的意义和价值，发展运算能力;

　　③有助于掌握处理，几何问题的一种方法，体会数形结合思想;

　　④有助于理解数学不同内容之间存在广泛的联系.

　　其中正确的共有( ).

　　A.1条

　　B.2条

　　C.3条

　　D.4条

　　参考答案：D

　　参考解析：略

　　8.数学归纳法的推理方式属于( ).

　　A.归纳推理

　　B.演绎推理

　　C.类比推理

　　D.合情推理

　　参考答案：B

　　参考解析：略

　　二、简答题(本大题共5小题，每题7分，共35分)

　　参考解析：

　　(2)在该变换条件下，①不变的性质:都是中心对称图形和轴对称图形，都是在某条件下点的轨迹所形成的对称图形;②变化的性质:图形形态发生了变化，不再以原点为中心点，不再与x轴和y轴相交，图形距离中心点的距离都相等。

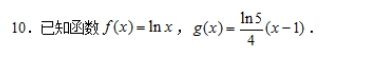
　　(1)求f(x)和g(x)围成的平面区域的面积.

　　(2)求0≤y≤f(x), 1≤x≤3,绕y轴旋转的体积.

　　查看答案

　　11.一个袋子里有8个黑球，8个白球，随机不放回连续取球5次，每次取出1个球，求最多取到3个白球的概率.

　　参考解析：

　　12.给出数学文化的内容，请举出数学课堂中两个能够应用数学文化的例子.

　　参考解析：

　　数学是一门与概念、定理、公式相关的学科，教师在数学教学中渗透数学文化、设置与教学内容相关的且蕴含在现实生活中的数学文化、引导学生思考其中所隐含的数学知识和规律，对学生的数学学习具有巨大的帮助。例如:

　　(1)在学习《整数和负数》时，“负数” 概念对学生来说相对抽象。教师可以在教学中渗透数学文化史:中国是最早提出负数的国家，《九章算术》 是最早、最完整介绍负数的古书，人们在求解方程时经常会遇到小数减大数的情形，为便于求解，便创造了负数;在古代为区分正负数，数学家创造了一种方法:用不同颜色的算筹来表示正、负数;中国古代不仅提出了负数的概念，还提出了整套的正、负数的运算法则，这些法则沿用至今。教师在教学中融入数学文化，让学生了解概念产生的背景和意义，利用概念与生活的相通性可以帮助学生更直观地理解概念。

　　(2)在教学《勾股定理》时，可以从毕达哥拉斯到朋友家做客的故事入手:毕达哥拉斯是古希腊最为著名的数学家之-，相传2500年前，他到朋友家做客，发现朋友家用地板砖铺成的地面反映出了直角三角形的三边关系。毕达哥拉斯发现直角三角形的三边关系的故事为《勾股定理》的教学提供了问题引入，学生通过思考故事中隐含的规律，从而进行猜想假设，再加上教师的演示将定理变得具体形象，学生能够更容易地总结出直角三角形的三边关系，即勾股定理。探究勾股定理相关的数学文化史的过程蕴含了丰富的数学思想方法，这对学生理解定理极为有利。

　　将数学文化渗透到数学教学中,将教材内容与数学文化巧妙结合起来，从数学文化中延伸出数学概念和规律，可以帮助学生理解相关内容。数学文化中蕴含的故事具有较强的趣味性，还可以激发学生的学习兴趣。

　　13.简述数学建模的主要过程.

　　参考解析：

　　数学建模是运用数学思想、方法和知识解决实际问题的过程。建立和求解模型的过程包括:从现实生活或具体情境中抽象出数学问题，用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律，求出结果、并讨论结果的意义。具体如下:

　　(1)模型准备:了解问题的实际背景，明确其实际意义，掌握对象的各种信息。以数学思想来包容问题的精髓，数学思路贯穿问题的全过程，进而用数学语言来描述问题。要求符合数学理论，符合数学习惯，清晰准确。

　　(2)模型假设:根据实际对象的特征和建模的目的，对问题进行必要的简化，并用精确的语言提出一-些恰当的假设。

　　(3)模型建立:在假设的基础上，利用适当的数学具来刻划各变量常量之间的数学关系，建立相应的数学结构(尽量用简单的数学工具)。

　　(4)模型求解:利用获取的数据资料，对模型的所有参数做出计算(或近似计算)。

　　(5)模型分析:对所要建立模型的思路进行阐述，对所得的结果进行数学上的分析。

　　(6)模型检验:将模型分析结果与实际情形进行比较，以此来验证模型的准确性、合理性和适用性。如果模型与实际较吻合，则要对计算结果给出其实际含义，并进行解释。如果模型与实际吻合较差，则应该修改假设，再次重复建模过程。

　　三、解答题(本大题1题, 10分)

　　14.已知函数f(x)在闭区间[a,b].上连续，且f(a).f(b)<0,请用二分法证明f(x)在(a,b)内至少有一个零点。

　　参考解析：

　　证明过程见解析。

　　四、论述题(本大题1小题，15分)

　　15.有人认为目前的教学缺乏对中学生思维能力的培养，请谈一谈你的看法，并说一说在老师在教学中应该如何做。

　　参考解析：

　　现代教育观点认为，数学教学活动是数学活动的教学，即思维活动的教学。孔子说: “学而不思则罔，思而不学则殆”,养成良好的思维品质是教学改革中的一个重要课题，在数学学习中要使学生思维活跃，就要教会学生分析问题的基本方法，在如今的教育体制之下灌输式教学还是很常见，从而忽视了对学生学习思维的培养，这对于学生创新能力的培养是极其不利的，因此在教育体制改革的趋势之下，我们不仅要重视学生基本知识和基本技能的学习，更应该注重学生思维品质的培养。心理学家认为，培养学生的数学思维品质是培养和发展数学能力的突破口。思维品质包括思维的深刻性、敏捷性、灵活性、批判性和创造性，它们反映了思维的不同方面的特征，因此在教学过程中应该有不同的培养手段。

　　思维的深刻性既是数学的性质决定了数学教学既要以学生为基础，又要培养学生的思维深刻性。数学思维的深刻性品质的差异集中体现了学生数学能力的差异，教学中培养学生数学思维的深刻性，实际上就是培养学生的数学能力。数学教学中应当教育学生学会透过现象看本质，学会全面地思考问题，养成追根究底的习惯。

　　数学思维的敏捷性主要反映了正确前提下的速度问题。因此，数学教学中，一方面可以考虑训练学生的运算速度，另一方面要尽量使学生掌握数学概念、原理的本质，提高所掌握的数学知识的抽象程度。因为所掌握的知识越本质、抽象程度越高，其适应的范围就越广泛，

　　五、案例分析题(本大题1题, 20分)

　　16.在学习了“直线与圆的位置关系”后，一位教师让学生解决如下问题:

　　参考解析：

　　(1) 该同学的解法没有考虑直线L斜率不存在的情况，没有掌握数学当中分类讨论的思想和斜率的定义。正确解法①如上同学做题步骤，且过论当斜率不存在时，直线L方程为x=2符合题意;②第二种做法可以先求出切点坐标，然后再求方程，易知切点为

　　检索的速度也就越快。另外，运算速度不仅仅是对数学知识理解程度的差异，而且还有运算习惯以及思维概括能力的差异。因此，数学教学中，应当时刻向学生提出速度方面的要求，使学生掌握速算的要领。

　　为了 培养学生的思维灵活性，应当增强数学教学的变化性，为学生提供思维的广泛联想空间，使学生在面临问题时能够从多种角度进行考虑，并迅速地建立起自己的思路，真正做到举一反三”。教学实践表明，变式教学对于培养学生思维的灵活性有很大作用。

　　六、教学设计题(本大题1小题，30分)

　　17.普通高中课程标准2017版，对“导数的概念及其意义”提出的学习要求为:

　　①通过实例分析,经历由平均变化率过渡到瞬时变化率的过程，了解导数概念的实际背景,知道导数是关于瞬时变化率的数学表达，体会导数的内涵与思想。

　　②体会极限思想。

　　③通过函数图象直观理解导数的几何意义。

　　针对导数的概念及其意义以达到①，完成教学设计。

　　(1)设计教学重点(6分)。

　　(2)教学过程(导入、概念形成与巩固)，并写出设计意图(24分)。

　　参考解析：

　　(1)教学重点:深刻理解在一点处导数的概念，能准确表达其定义;注意

　　[设计意图]教学中遵循“学生为主体,教师为主导，训练为主线，发展思维为主旨”的“四主原则”。以恰当的系列活动为纽带，给学生创设自主探究、合作交流的时间与空间，引导学生经历数学知识再发现的过程，让学生在参与中获取知识，发展思维，感悟数学。

　　③巩固概念:利用导数定义求是数的几个例子

　　[设计意图]加深学生对导数内涵的理解，熟练应用导数的概念进行运算，提炼求导步骤由特殊到一般，完成思维的飞跃。通过具体例题的分析，加深学生对导数内涵的理解，体验数学在实际生活中的应用。